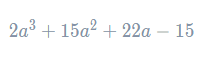This page contains the GCSE AQA Mathematics Multiples and factors Questions and their answers for revision and understanding Multiples and Factors.
Multiplication is a form of repeated addition, i.e. multiplying numbers amounts to adding several copies of a number together. Division is the opposite of multiplication, it amounts to finding out how many lots of one number go into another number. Both of these operations can get quite difficult when we have to deal with bigger numbers, so we’re going to look at 2 methods of multiplication and 2 methods of division for dealing with trickier situations.
Multiplication
The two multiplication methods we will see are the grid method and long multiplication.
Example: Work out 23×281 using the grid method and long multiplication.
The grid method involves splitting each number into 1s, 10s, 100s and so on, and writing each component of one number along the top of a grid, and each component of the other number down the left-hand side, as seen on the left.

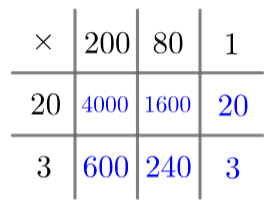
Then, we fill all the squares of the grid by multiplying each bit of one number by each bit of the other. So, the top left square will be 20×200=4000, and the bottom left one will be 200×3=600, and so on. Carrying this on with the rest of the multiplications and you get the filled grid on the right. Now, what remains is to add together all the numbers in blue. Along the top row, we get: 4000+1600+20=5,620, and along the bottom row we get: 600+240+3=843. Then, by whichever method you prefer, add together these two values to get
5,620+843=6,463
This is precisely the result of the multiplication, i.e. 23×281=6,463.
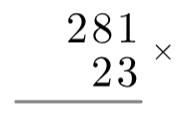
Long multiplication involves the same idea of multiplying each component at a time, but it’s structure is a little more compact. To start it, write the bigger number over the smaller one, making sure that the 1s are above each other, the 10s are above each other and so on. Keeping everything in the right column matters a lot here.
Then, we want to multiply each component of 281 by the “3” part of 23 and write the results of the multiplications under the grey line.31×3=3, so we write a 3 in the 1s column under the grey line. Then,8×3=24, but we can’t write “24” in one column. What we do is write the 4 in the 10s column and carry the two over to the 100s column. Then, 2×3=6, but we carried over an extra 2, so we write 6+2=8 in the 100s hundreds column (see: right).
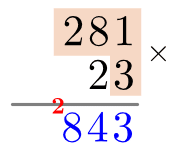
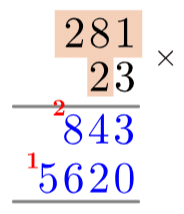
Now, we do everything we just did but this time, multiply each component of 281 by the “2” part of 23. The only difference is because the 2 represents a 20, everything is shifted one space to the left and a zero is put in the 1s column. For the completed step, using same methods as before, see: left.
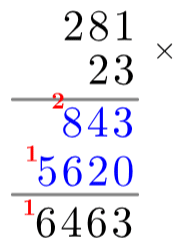
Finally, we add together the blue numbers and write the final answer underneath the second grey line. The answer (as we already know) is 5,620+843=6,463. For the completed process, see: right.
Have a go at both of these methods and decide which you prefer – it’s completely up to you which one you use.
Division
The two division methods we will see are long division and short division.
Example: Use long and short division to work out 288 div 9288÷9.

For long division, draw a rotated L-shape with the number we’re dividing (the dividend) on the inside, and the number we’re dividing by (the divisor) on the outside.
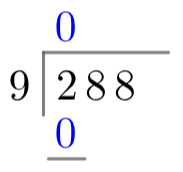
Now, see how many times the divisor, 9, goes into the first digit of the dividend, 2. 9 goes into 2 zero times, so we write a zero on top of the line above the 2. Then, we multiply this value by the divisor, 9times 0=09×0=0, and write the answer below the two (see: left).
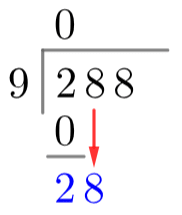
Next, we subtract the number below the 2 (zero) from 2 and write the answer underneath the zero. After that, we move onto the second digit of the dividend, 8, and bring it down to sit next to the result of this subtraction (see: right).
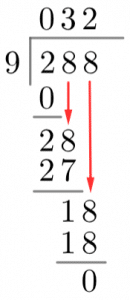
We’ve now seen all the steps involved, we just have to repeat them as many times as necessary until the division is complete. So, now we ask how many times our divisor, 9, goes into 28. The answer is 3, so we write a 3 above the top grey line, in line with the second digit of the dividend. Next, we multiply this 3 by the divisor to get 27 and write the 27 underneath 28. Next up, we subtract 27 from 28 to get 1, write the 1 underneath, bring the next digit of the dividend down and repeat this whole process. Once your divisor has 3 digits, then you just have to one final subtraction to determine the remainder. As you’ll see on the left, this gives us the answer: 288÷9=32 with no remainder.
For short division, we begin with exactly the same setup. From there, we ask how many times 9 goes into 2 and write the answer, zero, above the line, as before. Then, we write the remainder of this division, 2, in the gap just before the next digit of the dividend (see: right). Then, we ask how many times the divisor goes into the number formed by that remainder and the next digit, which here is 28. So, 9 goes into 28 three times with a remainder of 1, meaning we write a 3 above the line and a 1 in the gap before the third digit of the dividend. This process is exactly the same and repeats until we get to the end of the number (see: left).
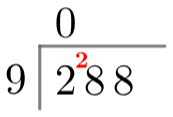
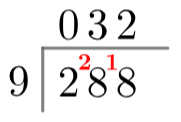
If the divisor doesn’t fit perfectly into the divided, you can either stop once you get to the end and take the final remainder to be the remainder of the whole division, or you can put in a decimal point and keep going until you’re satisfied with how many decimal points you have.
As with multiplication, try both these methods and see which one is better for you.
To multiply two fractions together, simply multiply the numerators together, and then multiply the denominators together.
Example: Evaluate 3/4×2/11. Write your answer in its simplest form.
The result of multiplying two fractions together will be a fraction. The numerator will be the product of the two numerators, and the denominators will be the product of the two denominators.
3/4×2/11= 3×2/4×11=6/44
Cancelling out a factor of two from top and bottom, we get the answer (in its simplest form) to be
6/44=3/22
Example: Evaluate 4×3/7
To multiply a whole number by a fraction, remember that any number divided by 1 is just itself. So, we can write
4=4/1
Therefore, the multiplication becomes
4/1×3/7=4×3/1×7=12/7
You may see that what happens when you multiply a whole number by a fraction, is that the number is multiplied only by the numerator. If you feel confident, you can just go right ahead and multiply the number by the numerator and avoid the intermediate steps.

To multiply a mixed number by a fraction, first convert the mixed number to an improper fraction.
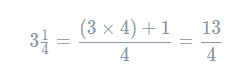
Now we can do the multiplication as usual.
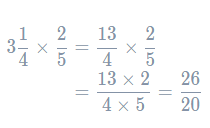
This fraction could be simplified, but as the question doesn’t ask us to, there’s no need.
Note: if negative numbers are involved, normal rules of multiplying apply:
1. If you multiply one positive fraction with one negative fraction, the answer should be negative.
2. If you multiply two negative fractions together, the answer should be positive.
Expanding Single Brackets
We often come across mathematical expressions with brackets in them. Sometimes it’s useful to have them in brackets, but sometimes we’d rather not have them at all. The process by which we remove bracket is called expanding (or multiplying out) the brackets.
The first thing to understand about expanding brackets is this: is that if you ever see a number, algebraic term, or algebraic expression written directly before a bracket, such as 5(4+b), then this means that everything inside the bracket is being multiplied by what’s in front of it. So, when you are expanding a single bracket, make sure that whatever is out front gets multiplied by everything on the inside.
Example: Expand 2a(4+a).
As stated, everything inside the bracket, 4 and an a, is being multiplied what’s outside it, 2a. So, the expansion of this bracket looks like
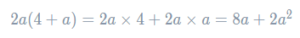
Thus, the result of the expansion is 8a + 2a
Example: Expand
![]() .
.
Just as before, we will multiply what’s outside the bracket 5yx2, by everything inside the bracket. So, the bracket expansion looks like
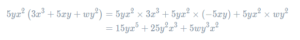
Thus, the result of the expansion is
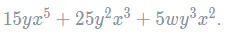 .
.
Expanding Double Brackets
When expanding double brackets, the idea is similar: we need to multiply each of the things in the first bracket is by each of the things in the second bracket. One method of making sure you’ve all done all the requisite multiplication is by using FOIL.
Example: Expand and simplify (x+3)(x−4).
FOIL is an acronym that stands for First, Outer, Inner, Last. First tells us to multiply the first terms in each bracket together; Outer tells us to multiply the outer two terms; Inner tells us to multiply the inner two terms; Last tells us to multiply the last terms in each bracket.
A good way to track the multiplication you’re doing is by drawing a line between each term once you’ve multiplied it. Here, we’ve added a red line to account for each multiplication.
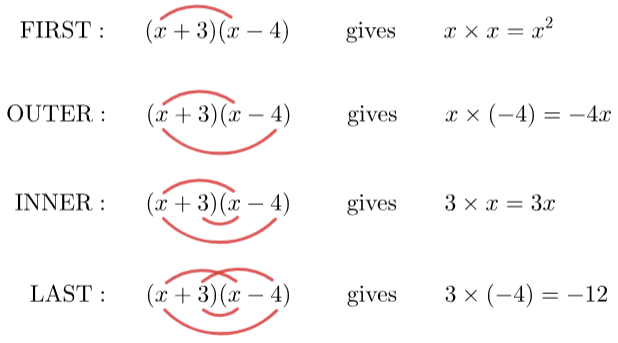
Once you have 4 red lines, you have completed the requisite multiplications. Now we need to add together the results of those multiplications:
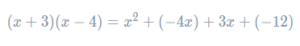
Finally, we must collect like terms to satisfy the “simplify” part of the question. We get the final answer to be
x2−x−12.
Naturally, as you get better you won’t have working out as extensive as this for each expansion, but it is definitely a good idea to keep track of the expansion by adding in the (red) lines as you go along.
Example: Expand and simplify (m + 8)(6 – m).
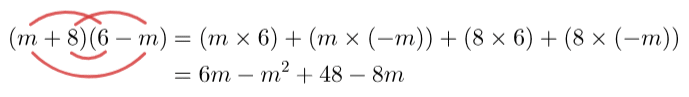
Multiplying Out Triple Brackets
Previously, we’ve seen how to expand single and double brackets – if you don’t remember, so now we’re going to look at expanding triple brackets. Fortunately, this new kind of expansion isn’t really a new kind at all. The ideas are much the same as when we expanded double brackets, it’s just the messier algebra that makes it tricky. Let’s take a look.
Example: Expand and simplify (x−2)(x+1)(x+3).
To do this, we’re first going to expand the second two brackets, (x+1)(x+3), as this is a familiar process. You can use whichever method you prefer to expand these brackets fully, here we’re going to follow the FOIL method of multiplying the First terms in each bracket, then the Outer terms, then the Inner terms, and finally the Last terms in each bracket. So, we get
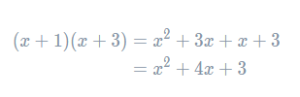
Now we’ve expanded these two brackets, we can rewrite the original expression, replacing the last two brackets with their expansion. Doing so, we get
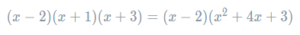
This is now a double bracket expansion, albeit one with a more complicated second bracket than usual. As mentioned, the principle is the same as usual – we must remember to multiply every term in the first bracket by every term in the second. Sadly, there is no handy acronym like FOIL that we can use in this case (why not try to come up with one?), so to make sure that we’ve done all requisite multiplications it helps to draw lines joining each pair of terms you’ve multiplied.
Here we will multiply the xx in the left-hand bracket by every term in the right-hand bracket, and then multiply the -2 in the left-hand bracket by every term in the right-hand bracket.
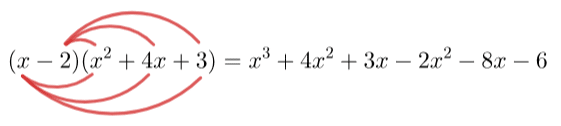
This looks like:
Another way to make sure you’ve done all the requirements is: when you are multiplying a bracket with 2 terms by a bracket with 3, the result should always have 6 terms. Now, we must simplify our answer, so collecting like terms, we get

This is the final result of the expansion.
There are no further methods or tricks you should know for this topic, the process will always be the same as this example. The main rule is to take your time – the algebra is messy and there are plenty of places to mess up, so be careful with it.
Example: Expand and simplify (a+5)(2a−1)(3+a).
Firstly, we expand the second two brackets into a normal quadratic. Using FOIL, we get
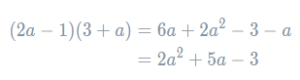
Then, replacing the second two brackets with their expanded version, we can rewrite the original expression:
![]()
We will now expand these two brackets, first multiplying the aa in the left-hand bracket by everything in the right-hand bracket, and then multiplying the 5 in the left-hand bracket by everything in the right-hand bracket. Doing so, we get
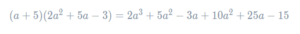
A quick count shows that this expression has 6 terms, which means we’re probably all good so far. What remains is to collect like terms. Doing so, we get the simplified expansion to be