This page contains the GCSE AQA Mathematics 3-dimensional Questions and their answers for revision and understanding 3-dimensional.
The volume of a 3D shape is how much space it takes up. You are expected to know how to work out the volumes of a bunch of different shapes, and some of these will come with a formula attached to the question, and some won’t:
- You will have to remember how to find the volumes of: prisms and pyramids.
- You will be given the formulae for finding the volumes of: cones and spheres.
Here, we’ll go through a series of examples of how to work out (and work with) different volumes, clearly outlining the formulae that you don’t have to remember, and the ones you don’t.
Example: Below is a triangular prism. The triangular face has base 6cm and perpendicular height 5cm. The prism has length 3.5cm. Work out the volume of the shape.

The formula for the volume of a prism is
volume of prism = area of cross section × length
This is for any prism, including cuboids & cylinders, and you do have to remember this formula. In this case, the cross section is a triangle, so we need to multiply the area of the triangle by the length. We get:
area of cross section =1/2×5×6=15cm2
Therefore,
volume of the prism =15×3.5=52.5cm3.
Example: Below is a square-based pyramid. The base has side-length 14mm and the pyramid has perpendicular height 25mm. Work out the volume of the pyramid.

The formula for the volume of a pyramid is
volume of pyramid =1/3 area of base × perpendicular height
This is for any pyramid with any shape of base, and you do have to remember this formula. In this case, the base is a square, so we have to find one third of the area of the square times by the height. We get:
area of base =142=196mm2
Therefore,
volume of the pyramid =1×196×25=1633.3mm3
Technically, a cone is a type of pyramid, and can use this method to work out its volume, but you are given the formula for the volume of a cone (if you need it in the question).
In this next example, we’ll use a volume formula to find a missing dimension – a common question.
Example: Below is a sphere with volume 2,100cm3. Work out the radius to 2sf. The formula for the volume of a sphere is 4/3πr3.
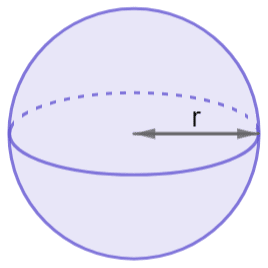
So, we are given the formula, as you would be in an exam question. Now, we know the volume is 2,100, so to find r (the radius) we must set the formula we’ve been given equal to 2,100 and rearrange for r. So, we get
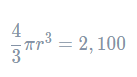
Firstly, multiply both sides by 3 to get
![]()
Then, we will divide both sides by 4pi4π to get
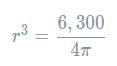
Finally, to find rr, we will get rid of the power of 3 by cube rooting both sides. Putting this into a calculator, we get

The final example will be a composite shape, which is a shape that is a combination of multiple different shapes. In reality, if you look around you’ll see that most objects aren’t just one shape, they’re a combination. As a result, this is a popular style of question.
Example: The shape below was made by attaching a cone to the top of a cylinder. The base of the cylinder has radius 4mm, the height of the cylinder portion is 3mm, and the height of the cone portion is 5.5mm. The formula for the volume of a cone is Work out the volume of the whole shape to 1dp.
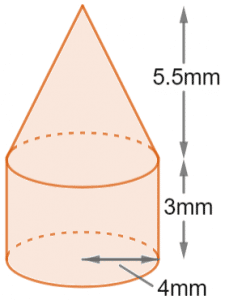
So, to work out the volume of the shape, we need to work out the two volume separately.
Firstly, the cylinder is a type of prism, so we know we need to multiply the area of the cross section by its length. Here, the cross section is a circle with radius 4mm, and the length of the cylinder is 3mm, so we get
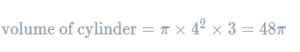
We’ll worry about the rounding at the end. Next, we have to work out the volume of the cone part, and fortunately the person who wrote the question (me) has been kind enough to give us the formula for a cone/it’s there because the exam boards decided it would be.
So, h is the height of the cone, which we know to be 5.5, and r is the radius of the cone, which is the same as that of the base: 4mm. Therefore, we get
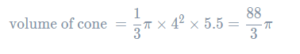
Then, the volume of the shape is the sum of these two answers:

