This page contains the GCSE AQA Mathematics laws of indices factors Questions and their answers for revision and understanding laws of indices.
There are three rules of indices (or laws of indices) which you have to know and be able to apply to problems involving both numbers and algebra. For any numbers, x, m,x,m, and nn, those three rules are
- The multiplication law – when you multiply terms, you add the powers:
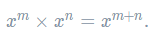
- The division law – when you divide terms, you subtract the powers:
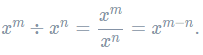
- The power law – when you take a power of a term already with a power, the powers are multiplied:
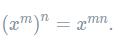
These laws don’t appear from nowhere. For example, let’s consider what happens if we do
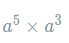
If we write this out as individual multiplications, it becomes
![]()
The left-hand bracket is a and the right-hand bracket is a^3a3. How many times is aa being multiplied by itself? Counting, we see that aa is repeated 5+3=8 times in the expression. So, we get that
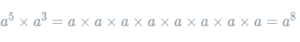
In mathematics, it’s important not to take things for granted. It’s a good exercise to try and figure out why the other two laws also make sense.
Example: Work out the value of
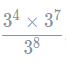
If we tried to work out 38 without a calculator, it would take a long time. Fortunately, the laws of indices can make our lives a lot easier. Firstly, let’s consider the numerator. Applying the multiplication law, we get that
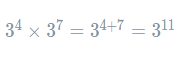
So, the calculation becomes
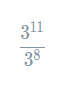
This is a division, so applying the division law, we get
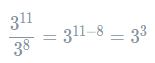
Now, the expression has become something that’s not too tricky to handle, and so the final answer is
![]() .
.
Note: problems like this can only be simplified if the base is the same, i.e. we can do ![]() , but there is no good way to simplify since their bases are different.
, but there is no good way to simplify since their bases are different.
Example: Write in its simplest form.
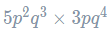
To simplify this expression, we must recognise that it can be broken up into parts, i.e. we can write
![]()
Then, we can rearrange the terms of this multiplication to make it
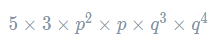
Firstly, 5×3=15. Then, the rest of the terms can be simplified using the multiplication law. Recalling that p=p1, we get that
![]()
Therefore, the expression simplifies to
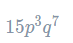
This application of the multiplication law is used all the time when you expand brackets. With practice, you should be able to perform this process quite quickly.
This next example is a little trickier, so don’t worry if it isn’t so obvious at first.
Example: Write as a power of 2, and hence evaluate the expression. (No calculator)
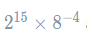
As mentioned earlier, the laws of indices only work if the things you’re multiplying/dividing have the same base, and these two things certainly don’t. However, with some subtle manipulation, we can make it so that they do.
The first part of the expression is a power of 2, whilst the second part is a power of 8. The key observation here is realising that 8 is actually a power of 2, specifically it is 2^3. This means we can write the second term in the expression as
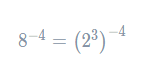
Now, this is in the appropriate form for us to apply the power law. Doing so, we get
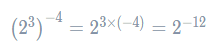
This is extremely helpful, because it is now also a power of two! So, because the whole expression can be written as
![]()
we can use the multiplication law. Hooray! So, we get
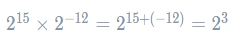
Thus, we have written the expression as a power of 2. Evaluating the expression: 2^3, we get 2times2=8 , = 2×2×2=8.
Note: if you’re taking the higher paper, there’s no reason why these types of questions can’t include fractional powers. That said, the ideas are exactly the same, you just have to be more careful with your calculations, since fractions make everything a bit more effort.
